CLASES EN LÍNEA 

PLATAFORMA GOOGLE CLASSROOM

NOMBRE DE LA CLASE: LA PARÁBOLA 

CÓDIGO: oza6gxl

PLATAFORMA VIDEOCONFERENCIA TELMEX

TEMA: LA CIRCUNFERENCIA COMO LUGAR GEOMÉTRICO

TEMA: LA CIRCUNFERENCIA COMO LUGAR GEOMÉTRICO

OBJETIVO: Desarrollar habilidades de visualización, representación, abstracción y razonamiento través del estudio de alguno de los temas propuestos para ampliar su cultura matemática.

FECHA: Nezahualcóyotl, Edo. de México. 2 de abril de 2020

FRASE DE LA SEMANA: "No estudio por saber más, sino por ignorar menos."          Sor Juana Inés de la Cruz

 

VER LOS VÍDEOS Y ANOTAR SU CONTENIDO EN EL CUADERNO DE APUNTES. ESTUDIAR Y REPASAR EL EJERCICIO.

INDICACIONES 

VERÁN LOS VÍDEOS QUE SE SUBIERON Y ANOTARÁN EL CONTENIDO DE LOS VÍDEOS.

LOS EJEMPLOS Y EJERCICIOS SE ANOTARÁN EN EL CUADERNO DE APUNTES. 

SE MANDARÁ POR CORREO, SE ESCANEARÁ SUS APUNTES, LETRA CLARA POR FAVOR

CORREO: tareasmatematicas_patria@hotmail.com

LA CIRCUNFERENCIA COMO LUGAR GEOMÉTRICO

TEMA: LA CIRCUNFERENCIA COMO LUGAR GEOMÉTRICO

OBJETIVO: Desarrollar habilidades de visualización, representación, abstracción y razonamiento través del estudio de alguno de los temas propuestos para ampliar su cultura matemática y profundizar en el  conocimiento y aplicación de la temática seleccionada por el profesor.

FECHA: Nezahualcóyotl, Edo. de México. 1 de abril de 2020

FRASE DE LA SEMANA: "No estudio por saber más, sino por ignorar menos."          Sor Juana Inés de la Cruz 

VER LOS SIGUIENTES VÍDEOS Y ANOTAR EN EL CUADERNO EL CONTENIDO DE LOS VÍDEOS.

INDICACIONES 

VERÁN LOS VÍDEOS QUE SE SUBIERON Y ANOTARAN EL CONTENIDO DE LOS VÍDEOS.

LOS EJEMPLOS Y EJERCICIOS SE ANOTARAN EN EL CUADERNO DE APUNTES. 

SE MANDARÁ POR CORREO, SE ESCANEARÁ SUS APUNTES, LETRA CLARA POR FAVOR

CORREO: tareasmatematicas_patria@hotmail.com

LUGARES GEOMÉTRICOS Y ECUACIONES DE LAS CÓNICAS.

TEMA: INTRODUCCIÓN A LUGARES GEOMÉTRICOS Y ECUACIONES DE LAS CÓNICAS. 

OBJETIVO: 

Desarrollar habilidades de visualización, representación, abstracción y razonamiento través del estudio de alguno de los temas propuestos para ampliar su cultura matemática y profundizar en el conocimiento y aplicación de la temática seleccionada por el profesor. FECHA: Nezahualcóyotl, Edo. de México. 30 de marzo de 2020 FRASE DE LA SEMANA: "No estudio por saber más, sino por ignorar menos."          Sor Juana Inés de la Cruz  SE PROPORCIONARÁ UN LINK DONDE VERÁN EL TEMA DE HOY. REALIZARÁN UNA PRESENTACIÓN EN POWER POINT DE LOS LUGARES GEOMÉTRICOS SERÁ UN ORGANIZADOR GRÁFICO https://prezi.com/gmtjkai5gwva/lugares-geometricos-y-conicas/ INDICACIONES  HARÁN UN ORGANIZADOR GRÁFICO EN POWER POINT, SERÁ A MODO DE RESUMEN DE LOS LUGARES GEOMÉTRICOS. SE MANDARÁ POR CORREO, SE REQUIERE IMÁGENES Y ECUACIONES CORREO: tareasmatematicas_patria@hotmail.com TAMBIÉN HAY INFORMACIÓN EN EL LIBRO DE TEXTO   Capítulo 23   PÁGINA 338 - 348 FECHA LIMITE 2 DE ABRIL

TEMA: DATOS BIVARIADOS: DIAGRAMA DE DISPERSIÓN 

OBJETIVO: 

Analizar y realizar representaciones gráficas provenientes de fuentes informativas, que ilustren el comportamiento de un fenómeno, para describirlo, interpretarlo, formarse una opinión crítica y en su caso, tomar decisiones.

FECHA: Nezahualcóyotl, Edo. de México. 25 de marzo de 2020

FRASE DE LA SEMANA: “Un ser no está completo hasta que no se educa.”  
Horace Mann

VER LOS SIGUIENTES VÍDEOS Y HACER ANOTACIONES EN EL CUADERNO 

INDICACIONES: 

VER LOS VÍDEOS Y HACER ANOTACIONES EN EL CUADERNO. 

CORREO: tareasmatematicas_patria@hotmail.com

Deberán escanear su apunte y la tarea en PDF, (FORZOSAMENTE EN PDF)  que se dejó y mandarla al correo de tareas 

con Nombre  completo del Alumno y grupo. 

TAREA:

REALIZARÁN UNA TABLA DE DATOS, OBTENDRÁN UN DIAGRAMA DE DISPERSIÓN. SIGUIENDO LOS PASOS DE LOS VÍDEOS

LO HARÁN EN EXCEL Y LA MANDARAN POR CORREO CON SU NOMBRE Y GRUPO.

REQUIERO LA TABLA CON DATOS QUE USTEDES PUEDEN INVENTAR Y SU GRÁFICA DE DISPERSIÓN. 

TEMA: DATOS BIVARIADOS: DIAGRAMA DE DISPERSIÓN CLASE 2

TEMA: DATOS BIVARIADOS: DIAGRAMA DE DISPERSIÓN 

OBJETIVO: 

Analizar y realizar representaciones gráficas provenientes de fuentes informativas, que ilustren el comportamiento de un fenómeno, para describirlo, interpretarlo, formarse una opinión crítica y en su caso, tomar decisiones.

FECHA: Nezahualcóyotl, Edo. de México. 24 de marzo de 2020

FRASE DE LA SEMANA: “Un ser no está completo hasta que no se educa.”  
Horace Mann

DESCARGAR ACTIVIDAD DE INICIO

Datos Bivariados

Se llaman datos bivariados a aquellos que provienen de dos variables medidas al mismo tiempo sobre cada individuo. Por ejemplo: Edad y Género, Escolaridad e Ingreso, Peso y Estatura, etc. Cuando los datos bivariados provienen de dos variables cuantitativas resulta de interés estudiar la relación que guarda una con la otra. La relación puede ser de muy distinta naturaleza: lineal, cuadrática, exponencial, logarítmica, trigonométrica, etc. En estadística la relación que nos interesa es la Relación Lineal, por lo que se llevan a cabo Análisis de Correlación Lineal y de Regresión Lineal El análisis de correlación, se usa para medir la fuerza de asociación entre las variables. El objetivo medir la covarianza que existe entre esas dos variables numéricas. El análisis de regresión se usa con propósitos de predicción. Se busca desarrollar un modelo estadístico útil para predecir los valores de una variable dependiente o de respuesta basados en los valores de al menos una variable independiente o explicativa. Ejemplo Se decidió examinar la relación entre la estatura, (en metros), y el peso, (en kilogramos), a partir de una muestra de 12 alumnas de cierta escuela. 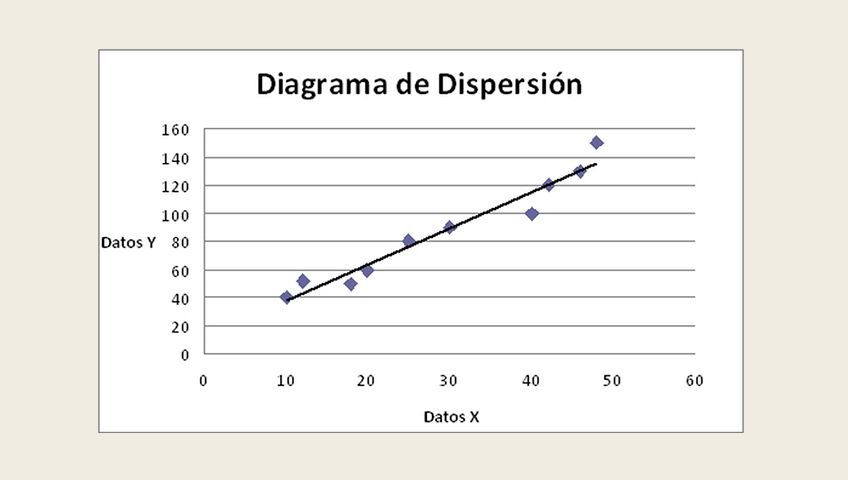Los datos se muestran en la siguiente tabla: Diagrama de Dispersión El diagrama de dispersión permite analizar si existe algún tipo de relación entre dos variables. Por ejemplo, puede ocurrir que dos variables estén relacionadas de manera que al aumentar el valor de una, se incremente el de la otra. En este caso hablaríamos de la existencia de una correlación positiva. También podría ocurrir que al producirse una en un sentido, la otra derive en el sentido contrario; por ejemplo, al aumentar el valor de la variable x, se reduzca el de la variable y. Entonces, se estaría ante una correlación negativa. Si los valores de ambas variable se revelan independientes entre sí, se afirmaría que no existe correlación. El diagrama de dispersión es una herramienta gráfica qe ayuda a identificar la posible relación entre dos variables. Representa la relación entre dos variables de forma gráfica, lo que hace más fácil visualizar e interpretar los datos. De otro lado, calculando el coeficiente de correlación entre dos variables, permite cuantificar el grado de relación entre ambas, así como su signo. El valor de este coeficiente puede estar comprendido entre −1 y 1. Cuando toma un valor próximo a −1, la correlación es fuerte y negativa. Si el valor es cercano a +1, la correlación es fuerte y positiva. Si el coeficiente de correlación lineal presenta un valor próximo a 0, la correlación es débil. Un coeficiente de 0 indicaría independencia total entre ambas variables. A su vez, un coeficiente de correlación lineal de 1 ó de -1 señalaría que entre ambas variables hay dependencia funcional, positiva o negativa según el signo del coeficiente. Esta correlación puede señalar, pero no por ello probar, una relación causal, es decir, no predice relaciones causa – efecto, sino que muestra la intensidad de la relación entre dos variables. Por lo tanto, es importante no apresurarse a obtener conclusiones sobre la relación entre las variables, ya que puede ser otra tercera que afecte a la relación. VER EL SIGUIENTE VÍDEO Y ESTUDIAR QUE ES UN DIAGRAMA DE DISPERSIÓN. HACER ANOTACIONES DEL VÍDEO EN SU CUADERNO. INDICACIONES:  COPIAR EN SU CUADERNO LA TEORÍA. VER LOS VÍDEOS Y TAMBIÉN COPIAR LAS EXPLICACIONES Y EJEMPLOS QUE SE ESTÁN DANDO EN  EL VÍDEO. CORREO: tareasmatematicas_patria@hotmail.com Deberán escanear su apunte y la tarea en PDF, (FORZOSAMENTE EN PDF)  que se dejó y mandarla al correo de tareas  con Nombre  completo del Alumno y grupo.  TAREA: ESCANEAR TU APUNTE Y MANDARLO POR CORREO FAVOR DE ESTUDIAR.

GRÁFICOS ESTADÍSTICOS PARA DATOS AGRUPADOS: HISTOGRAMA, POLÍGONO DE FRECUENCIAS Y OJIVA.

¡BUEN DÍA! ALUMNOS DEL 5010

FAVOR DE DESCARGAR CRONOGRAMA DE ACTIVIDADES DE LA MATERIA DE MATEMÁTICAS V "GEOMETRÍA ANALÍTICA "

¡DESCARGAR AQUÍ Y AHORA!

TEMA: GRÁFICOS ESTADÍSTICOS PARA DATOS AGRUPADOS: HISTOGRAMA, POLÍGONO DE FRECUENCIAS Y OJIVA.

OBJETIVO: 

Analizar y realizar representaciones gráficas provenientes de fuentes informativas, que ilustren el comportamiento de un fenómeno, para describirlo, interpretarlo, formarse una opinión crítica y en su caso, tomar decisiones.

FECHA: Nezahualcóyotl, Edo. de México. 23 de marzo de 2020

FRASE DE LA SEMANA: “Un ser no está completo hasta que no se educa.”  
Horace Mann

Un Histograma es la representación gráfica de una tabla de frecuencias. El histograma puede ser: de frecuencias absolutas, de frecuencias relativas, de frecuencias absolutas acumuladas y de frecuencias relativas acumuladas.

Más profundamente, el histograma de frecuencias es una representación visual de los datos en donde se evidencian fundamentalmente tres características: forma, acumulación o tendencia posicional y dispersión o variabilidad.

Un Polígono de Frecuencia es el nombre que recibe una clase de gráfico que se crea a partir de un histograma de frecuencia. Los histogramas emplean columnas verticales para reflejar las frecuencias, los polígonos de frecuencia se forman uniendo los puntos más altos de cada una de las columnas del Histograma.

Podemos observar que el polígono de frecuencia es la línea roja que une el centro de cada barra del histograma. Sólo se ha dejado el histograma para una mayor comprensión del concepto que se desea ilustrar.

Por último hablaremos de las Ojivas. 

Una Ojiva se utiliza para representar la frecuencia acumulada. Similar al Polígono de frecuencia, se forma o se construye uniendo los puntos más altos de cada columna pero de un Histograma que represente las Frecuencias Acumuladas.

Al estar construido en función de las frecuencias acumuladas permite ver cuántas observaciones se encuentran por encima o debajo de ciertos valores, en lugar de solo exhibir los números asignados a cada intervalo.

En este caso la Ojiva es la línea azul, pero se ha dejado el Histograma, por dos razones: (1) Para visualizar un histograma de Frecuencias Acumuladas; y, (2) Para tener una visión más clara de lo que representa la Ojiva.

En este ejemplo se visualiza claramente lo que se conceptualizó antes, por ejemplo, se puede ver rápidamente que hay 8 secciones con 39 alumnos o menos. 

Cabe destacar que las Ojivas también se pueden hacer a la inversa, comenzando con la mayor y terminando con la menor frecuencia.

Estos 3 tipos de gráficos son muy útiles y son fáciles de interpretar cuando estamos trabajando con tablas de frecuencia.

VER A CONTINUACIÓN LOS SIGUIENTES VÍDEOS QUE TRAE LA EXPLICACIÓN Y EJEMPLOS DE CADA GRÁFICO ESTADÍSTICO, COPIAR EN EL CUADERNO.

INDICACIONES: 

COPIAR EN SU CUADERNO LA TEORÍA.

VER LOS VÍDEOS Y TAMBIÉN COPIAR LAS EXPLICACIONES Y EJEMPLOS QUE SE ESTÁN DANDO EN  EL VÍDEO.

CORREO: tareasmatematicas_patria@hotmail.com

Deberán escanear su apunte y la tarea en PDF  que se dejó y mandarla al correo de tareas 

con Nombre  completo del Alumno y grupo. 

TAREA:  

Realizarán un organizador gráfico. (es un mapa mental)

Este organizador gráfico deberá estar en su cuaderno de apuntes como evidencia. mandar por correo